Fundamental Research in Membrane Separations

•  Membrane Contactor as Degasser: simulation studies

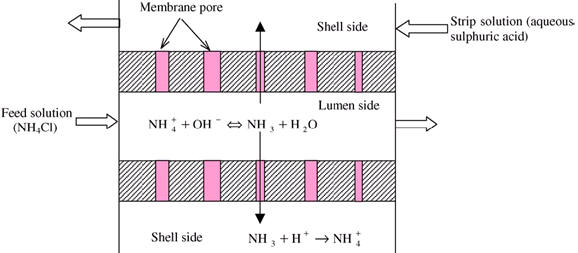
Membrane contactor as degasser (from water) can be either operated under vacuum or under LLE modes. Numerical simulations of mass transfer under different flow conditions have been attempted in order help to design the hollow fibre (hydrophobic polymer) based membrane contactor. 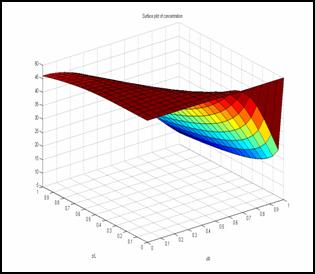Mathematical models have been developed* by using the resistances-in-series mass transfer system that takes into account boundary layers, membrane porosity, phenomenological considerations and mass balances of the membrane contactor. Simulation result shows the variation of concentration in both axial and radial direction.

    

  

 



 

* Amish Mandowara and Prashant K. Bhattacharya, “Membrane contactor as degasser operated under vacuum for ammonia removal from water: A numerical simulation of mass transfer under laminar flow conditions”, Computers Chem. Eng. (DOI information: 10.1016/j.compchemeng.2008.12.005).

 

• Pervaporation: membrane casting, separations and modelling

 



 

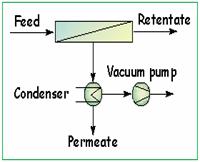
Pervaporation using hydrophobic membranes were observed to be promising for streams such as water contaminated with VOC's, organic-organic solutions, etc.

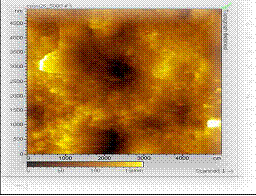
Membrane Casting: Several polymeric hydrophobic and hydrophilic dense membranes* were cast, modified and characterized through FTIR, XRD, 1H NMR, SEM, AFM, etc. Specific systems like hydrazine-water, alcohol-water, organic-organic, etc. have been studied. They were also assessed in comparison to commercial membranes for several typical chosen mixture separations.



 

 



 

 

 

 

* S. V. Satyanarayana, A. Sharma and P. K. Bhattacharya, “Composite membranes for hydrophobic pervaporation: Study with toluene-water system“, Chem. Eng. J., 102, 171 -184 (2004).

* S. V. Satyanarayana, P. K. Bhattacharya, “Pervaporation of Hydrazine Hydrate: Separation characteristics of membranes with hydrophilic to hydrophobic behaviour“, J. Membrane Sci., 238, 103 -115 (2004).

* Mrinal K. Mandal and P. K. Bhattacharya, "Poly (ether-block-amide) membrane for pervaporative separation of pyridine present in low concentration in aqueous solution", J. Membrane Sci., 286, 115-124 (2006)

* Mrinal K. Mandal and P. K. Bhattacharya, “Poly (vinyl acetal) membrane for pervaporation of benzene-isooctane solution”, Separ. Purif. Technol., 2007, 61 (2008) 332–340.

 

Real coded genetic algorithm and Model Development: Models have been developed to predict partial fluxes and selectivity's'. Real coded genetic algorithm has been used to optimize process parameters.

 

* Gopal R. Nemmani, Satyanarayana V. Suggala and Prashant K. Bhattacharya, “NSGA-II for Multiobjective Optimization of Pervaporation Process: Removal of Volatile organics from Water”, Ind. Eng. Chem. Res. (in press).

* Satyanarayana V. Suggala and Prashant K. Bhattacharya, “Real Coded Genetic Algorithm for Optimization of Pervaporation Process Parameters for Removal of Volatile Organics from Water“, Ind. Eng. Chem. Res., 42 (13), 3118 -3128 (2003)

* Nazish Hoda, Satyanarayana V. Suggala and Prashant K. Bhattacharya, “Pervaporation of Hydrazine – Water through Hollow Fiber Module: Modeling and Simulation“, Computers Chem. Eng., 30 (2), 202-214 (2005).

 

Roles of Permeant-Membrane Interactions: The membrane permeation of a component followed by its vaporization on the opposite face is governed by the solubility and downstream pressure. We studied and measured* the evaporative flux using dense membranes with different free volumes and different affinities (wettabilities and solubilities) for the permeant. Interestingly, the evaporative flux for different membranes vanished substantially (10-75%) below the equilibrium vapour pressure in the bulk. The discrepancy was larger for a smaller pore size and for more wettable membranes (higher positive spreading coefficients). This observation, which cannot be explained by the existing (mostly solution diffusion type) models of pervaporation, suggests an important role for the membrane-permeant interactions in nanopores that can lower the equilibrium vapor pressure.

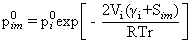
* A. Sharma, S. P. Thampi, S. V. Suggala and P. K. Bhattacharya, Pervaporation from a dense membrane: Roles of permeant – membrane interactions, Kelvin effect, and membrane swelling, Langmuir, 20(2004), 4708.

 

Location of vaporization using single component pervaporation:  A mathematical model* was developed assuming two zones inside the membrane; namely, liquid permeation and vapour permeation zones. Considering a pressure distribution across the thickness of the membrane, Kelvin equation (saturation vapour pressure gets modified inside the membrane due to permeant membrane interactions) proved to be useful in developing the model.

 

* Sumesh P. T. and P. K. Bhattacharya, “Analysis of Phase Change during Pervaporation with Single Component Permeation", Colloids and Surfaces A: Physicochemical and Engineering Aspects, 290, 263–272 (2006).

 

Positron annihilation study of pervaporation dense membranes*: Determination of free volume sizes is crucial to the understanding of pervaporation process. Positron annihilation technique has been developed into a powerful characterization tool for the study of free volume and free volume fraction in polymers. Long-lived components (lifetimes in the range 1.4 to 3 ns) were found, which were attributed to ortho-positronium (o-Ps) pick-off annihilations in free volumes. Free volume data is used to interpret the data of hydrazine hydrate separation by pervaporation.

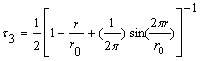
* S. V. Satyanarayana, V. S. Subrahmanyam, H. C. Verma, A. Sharma, P. K. Bhattacharya, “Application of positron annihilation: Study of pervaporation dense membranes“, Polymer, 47, 1300-1307 (2006).

• Development of Predictive Models for Flux Decline

Osmotic pressure controlled (for low MW solutes) and gel-layer controlled (for high MW solutes) flux decline have been examined by several workers with regard to modelling of UF flux behaviour. The applicability of either of these models is questionable for all operating conditions and solutes, especially in the intermediate range of molecular weights. Several predictive models have been developed overcoming these limitations.

The combined influence of osmotic pressure and gel-layer on the flux decline is to be expected during UF with solutes that display substantial osmotic pressure, and in addition, either form a true gel or a 'pseudo gel'. Such excellent models* can be useful for design purposes of UF and RO.

 

  



 

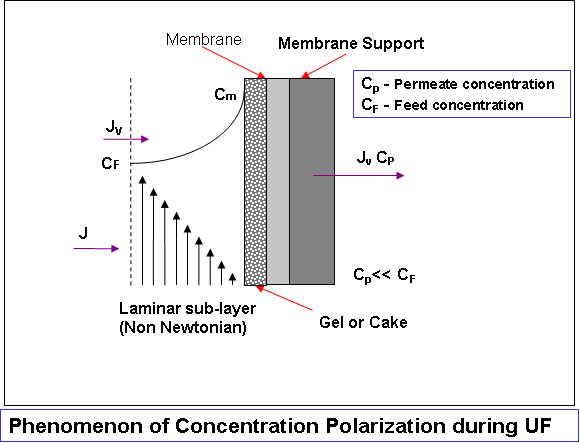
* C. Bhattacharjee and P. K. Bhattacharya, “Prediction of limiting flux in ultrafiltration of kraft black liquor“, J. Membrane Sci., 72, 137-147 (1992).

* S. Ganguly and P. K. Bhattacharya, “Development of concentration profile and prediction of flux for ultrafiltration in a radial cross flow cell“, J. Membrane Sci., 97, 185-198 (1994).

* S. De and P. K. Bhattacharya, “Flux prediction of black liquor in cross-flow ultrafiltration using low and high rejecting membranes“, J. Membrane Sci., 109, 109-123 (1996).

* S. Bhattacharjee, A. Sharma and P. K. Bhattacharya, “A unified model for flux prediction during batch cell ultrafiltration“, J. J. Membrane Sci, 111, 243-258 (1996).

 

• Role of Surface Interactions

The approach is to systematically incorporate the intermolecular interactions between solutes and membranes to develop models of flux decline. The role of solute-solute interactions is manifested in the variation of diffusivity and osmotic pressure, which govern the transport of the solution across the polarized layer and through the membrane. The solute-membrane interactions further affect the transport of solute and solvent through the membrane pores, thus predicting adsorption, fouling, etc. Models, thus, represent a marriage between the surface science and membrane separations aspects, and provide excellent agreement with experimental fluxes.

 

* S. Bhattacharjee, A. Sharma and P. K. Bhattacharya, “Surface interactions in osmotic pressure controlled flux decline during ultrafiltration“, Langmuir, 10, 4710-4720 (1994).

* S. Bhattacharjee, A. Sharma and P. K. Bhattacharya, “Estimation and influence of long range solute-membrane interactions in ultrafiltration“, Ind. Eng. Chem. Res., 35(9), 3108-3121 (1996). [Invited paper for the special issue in honour of Prof. E. Ruckenstein].

 

• Mass Transfer Coefficient with Suction

Sherwood number relations for the prediction of mass transfer coefficient, including the effect of suction, have been developed from first principles]. The proposed relations predict the permeate flux in RO and UF in an excellent manner. For other effluents, some empirical equations have also been developed.

 

  

 

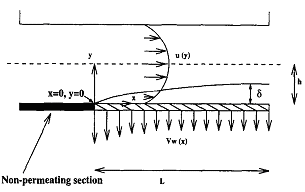
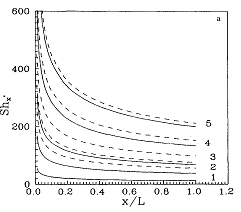
* S. De and P. K. Bhattacharya, “Mass transfer coefficient with suction including property variations in applications of cross-flow ultrafiltration“, Separ.Purif. Technol., 16, 61-73 (1999).

* S. De and P. K. Bhattacharya, “Prediction of mass transfer coefficient with suction in the applications of reverse osmosis and ultrafiltration“, J. Membrane Sci., 128, 119-131 (1997).

 

• Generalized Integral & Similarity Solutions for Concentration Profiles

In this exciting method, one has to solve only two ordinary differential equations and one non-linear algebraic equation, compared to solving around 700 coupled ordinary differential equations simultaneously in the detailed numerical solution. Still accuracy and generality of the problem are fully retained. The model can predict flux decline over time (for an unstirred) or over channel length (for a steady cross-flow system) as well as of the permeate concentration with time or channel length, if operating conditions are known.

 

* S. De, S. Bhattacharjee, A. Sharma and P. K. Bhattacharya, “Generalized integral and similarity solutions for concentration profiles for osmotic pressure controlled ultrafiltration“, J. Membrane, Sci., 130, 99-121 (1997).

Back